Deep Dive: Renjin's Vector Pipeliner
Radford Neal, the statistician behind pqR, has started a great conversation on a recent blog post that compares how pqR, Renjin, and Riposte defer and parallelize computation while evaluating R code.
In this post, I want to continue this conversation by going into a bit more depth about how Renjin's vector pipeliner works, some results we've achieved so far, and where we hope to go with it.
I think the best way is to look at one of the real-world use cases that informed its design.
Real World Use Case: Distance Correlation
One of the use cases where we really saw Renjin shine was in a data mining exercise for a large mobile operator where we wanted to find associations between sociodemographic variables and a large number of usage-pattern variables.
The usage-pattern variables, like "number of SMS' sent per month", or the "number of international calling minutes to South East Asian countries" often have far-from-normal distributions, with some percentage of the subscriber base zero, and then a long tail of extreme values.
For this reason, we wanted to use distance correlation, a relatively new measure of assocation that helps detect non-linear relationships between random variables, provided in the energy package.
Unfortunately, this is a case where the original GNU R interpreter has serious limitations. As soon as the number of observations grows beyond a few thousand, GNU R's memory usage explodes and computation grinds to a halt or crashes. The author has provided a C implementation as well, but it doesn't fare much better.
Renjin, on the other hand, outperforms GNU R on small samples by a factor of 2, and uses a fraction of the memory required by GNU R, allowing us to scale up to our target of 25,000 observations.
Here are the results of a little distance correlation benchmark that compares the runtimes of Renjin 0.7.0-RC6, GNU R-3.0.1 and pqR 2013-07-22 in seconds:
Runtimes (in seconds)
| n | GNU R | pqR | Renjin |
|---|---|---|---|
| 1000 | 5 | 3 | 3 |
| 2000 | 20 | 10 | 9 |
| 5000 | 120 | 79 | 52 |
| 6000 | 112 | 74 | |
| 7000 | 151 | 100 | |
| 8000 | 219 | 133 | |
| 10000 | 209 | ||
| 25000 | 1319 |
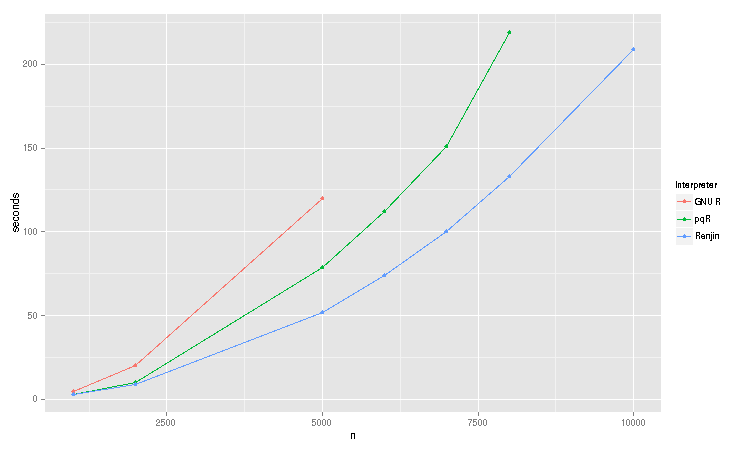
In this particular benchmark, Renjin outperforms GNU R by roughly half of the time as GNU R 3.0.1. For smaller sizes, Renjin and pqR are roughly even, but as the sample grows larger, Renjin starts to approach a 2x speed up as well.
More importantly, Renjin is able to handle sample sizes of up to around 25000 observations, a limitation currently imposed by Renjin's 32-bit indexing of arrays. (We'll see below that there is a distance matrix at the heart of the dcor function, which requires n^2 storage space)
GNU R runs out of memory at n = 6000, and pqR at n = 8000.
The Challenge
In the rest of this post, we'll look at how Renjin's design support this particular use case in terms of both performance and conservative memory use.
Let's take a look at the DCOR() function in the energy package: (some argument checking omitted for clarity)
function (x, y, index = 1)
{
x <- dist(x)
y <- dist(y)
x <- as.matrix(x)
y <- as.matrix(y)
n <- nrow(x)
m <- nrow(y)
dims <- c(n, ncol(x), ncol(y))
Akl <- function(x) {
d <- as.matrix(x)^index
m <- rowMeans(d)
M <- mean(d)
a <- sweep(d, 1, m)
b <- sweep(a, 2, m)
return(b + M)
}
A <- Akl(x)
B <- Akl(y)
dCov <- sqrt(mean(A * B))
dVarX <- sqrt(mean(A * A))
dVarY <- sqrt(mean(B * B))
V <- sqrt(dVarX * dVarY)
if (V > 0)
dCor <- dCov/V
else
dCor <- 0
return(list(dCov = dCov, dCor = dCor, dVarX = dVarX, dVarY = dVarY))
}
The central problem for GNU R lies in the first line: it calculates a distance matrix for the two variables, meaning that if we have two variables with 5,000 observations, GNU R will allocate 5,000^2 * 2 variables * 16 bytes = 762 mb of space.
For this algorithm, the memory requirements in GNU grow quadratically: for 10,000 observations we need 3GB, and for 50,000 observations we need 76 GB.
Lazy data Structures
Renjin, on the other hand, doesn't allocate any memory at all in this first step: for large vectors, it simply returns a view of the underlying data, computing the individual elements as they are needed.
The dist() function and the as.matrix.dist() both return Java objects that implement the DoubleVector interface and compute their elements on demand. To both R and Java code, the result of the dist() function looks exactly like any other vector, complete with a length and a set of attributes.
public class DistanceMatrix extends DoubleVector {
private Vector vector;
public DistanceMatrix(Vector vector, AttributeMap attributes) {
super(attributes);
this.vector = vector;
}
@Override
public double getElementAsDouble(int index) {
int size = vector.length();
int row = index % size;
int col = index / size;
if(row == col) {
return 0;
} else {
double x = vector.getElementAsDouble(row);
double y = vector.getElementAsDouble(col);
return Math.abs(x - y);
}
}
@Override
public int length() {
return vector.length() * vector.length();
}
}
Functions like ncol() or nrow() require no computation at all, as they rely on the length and dim attributes of our distance matrix, rather than any of the actual values.
How lazy can we be?
But of course having a nice distance matrix view doesn't help if we turn right around and have to allocate memory to store the result of a statement like d <- as.matrix(x)^index.
To avoid this type of allocation, any primitive function in Renjin can be tagged as @Deferrable to indicate that it has no side affects (called "pure" in
For primitive functions annotated with @DataParallel, Renjin generates a subclass of DoubleVector (example), and when an expression like x^3 is evaluated, Renjin will simply return an instance of the view which calculates its elements on demand, first as the value of the distance matrix cell, and then cubing it.
Deferring Reducer Operations
We also defer reducer operations like rowMeans() and mean(), not because of space considerations, but because deferring these operations as long as possible give us more of an opportuntity to implicitly parallelize them.
These kinds of operations, however, are expensive to compute, so they are stored internally not as views, but as memoized values.
In fact, in the example above of DCOR, we get all the way to the if() statement before Renjin will do any computation. At that moment, V points to a view which references another view which references... and so on. You can think of it as a directed computation graph:
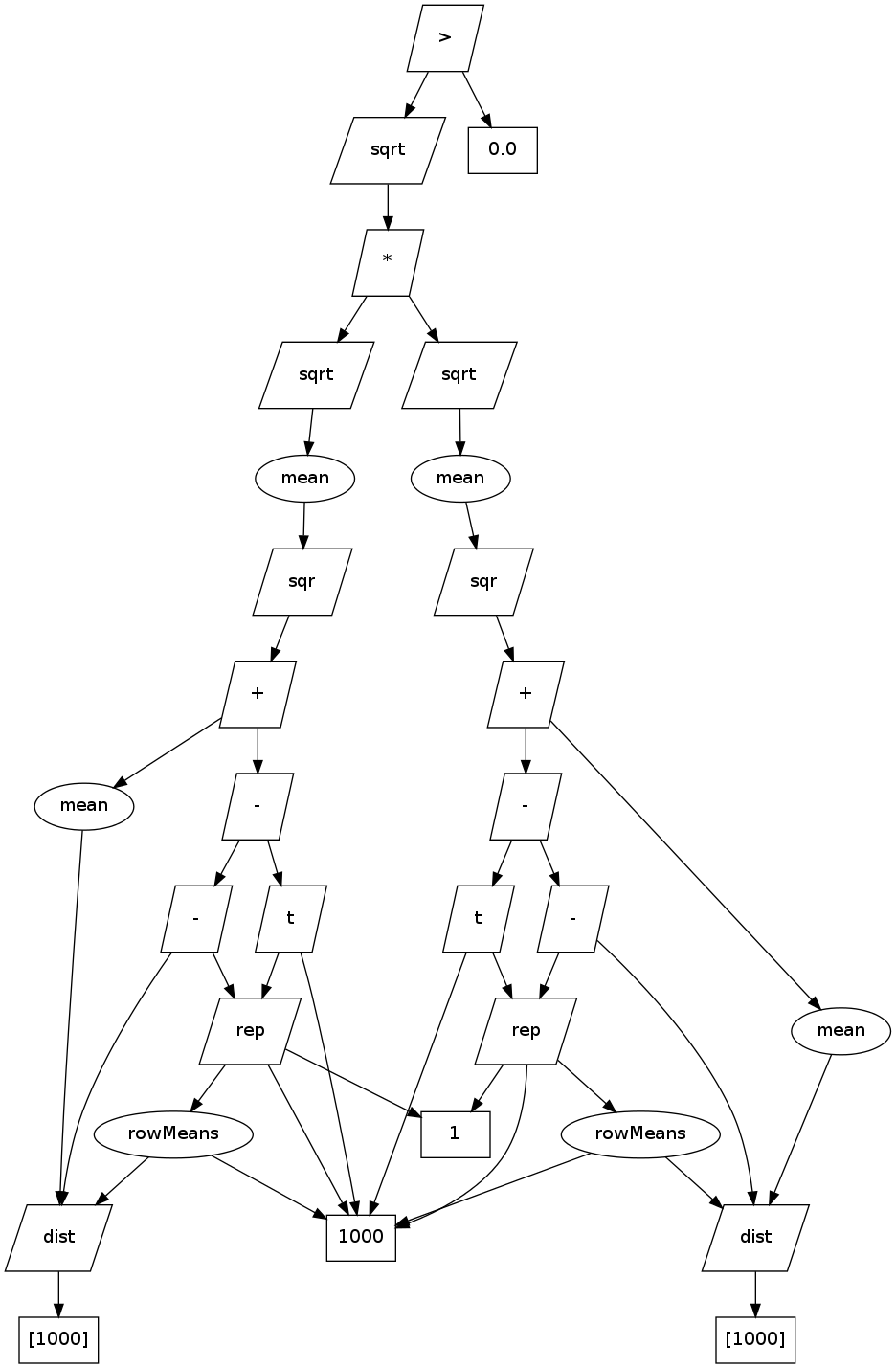
Where squares represent in-memory arrays, with lengths in brackets, paralellograms represent views, and ovals are reducer nodes.
When the value of V is needed by the if statement in order to know how to branch, Renjin will search the graph for reducer nodes and evaluate them in parallel.
Fusing Reducer Operators
In this example, all the real work is done by reducers, when we loop through all the values in a view to find their mean, or sum, or rowMeans.
Renjin's implementation of the mean() function looks something like this (essentially):
public static double mean(Vector x) {
double sum = 0;
for(int i=0;i!=x.length();++i) {
sum += x.getElementAsDouble(i);
}
return sum / (double)x.length();
}
Unfortunately, since we've built up these big trees of views, we get killed by all of these virtual getElementAsDouble() invocations. For large vectors, we can do much better by fusing all of the operations implied by our tree into a single, fully-inlined loop.
To look at a simple example, take the expression from the tree above mean(as.matrix(dist(x))). At runtime, Renjin inlines the body of the mean loop into straight line JVM byte code that might look like this in Java:
public static double mean(Vector distMatrix) {
// unwrap the underlying array
DoubleVectorArray vector = ((DistanceMatrix)distMatrix).getOperand();
double[] array = vector.toDoubleArrayUnsafe();
// set up the info we need for the distance matrix calculations
int matrix_length = array.length;
double sum = 0;
for(int i=0;i!=x.length();++i) {
int dist_matrix_row = index % size;
int dist_matrix_col = index / size;
double dist_matrix_value;
double x = array[row];
double y = array[col];
double dist_matrix_value = Math.abs(x - y);
sum += dist_matrix_value;
}
return sum / (double)distMatrix.length();
}
The difference between this fused code and tens of millions of virtual method invocations for the benchmark above is about 3 orders of magnitude.
Writing the bytecode for the fused reducers is relatively fast here to the runtime of the calculation, and is cached so that subsequent reducer operations on a graph of the same types can quickly reuse the previously compiled pipeline.
Beyond Arrays
In this example, all of our data is still in memory, and we execute all of the computations in-process, though with multiple threads.
In the future, the idea is to extend this approach to out-of-memory data structures and heterogenous computing environments, where the executor for these computation graphs is chosen based on where the underlying data resides.
In one case, you might have a DoubleVector implementation that points to a database table, and rather than pulling the data into the JVM's process from across the network, we might try to translate the computation graph above into SQL or a stored procedure to be executed within the database.
Perhaps simpler still, you can see the data residing on a Hadoop Distributed Filesystem (HDFS), and Renjin would select the vector backend that could compile the graph to a set of map/reduce jobs.
Limitations & Challenges
First caveat, this is example comes from one of our real projects where we added several optimizations to support the use case above. We replaced GNU R's distance function, for example, with one that returns a view rather than allocating an array. There are lots of other interesting functions that are not yet deferrable so your mileage may vary.
For me, this was an exciting case that demonstrated the kind of optimizations that are possible when you introduce a layer of abstraction between how you store data and the operations which act on that data.
Second, there are some cases where Renjin gets too good at deferring operation and we end up with enormous trees whose overhead far exceeds any computational gain.
For example:
x <- 1:100000
for(i in 1:1000) { x <- sqrt(x-mean(x)) }
print(mean(x))
I've added a quick fix to limit the growth of trees and force a calculation periodically, but I would really like Renjin to properly understand this loop and the dependency it involves between iterations and optimize accordingly.
Since most of Renjin's inspiration comes from the functional programming community, I'd be interested to see how the Glassgow Haskell Compiler, for example, handles a recursive definition like the one above.
That fortunately, will be the subject of next week's deep dive when Renjin's JIT compiler gets merged into the master branch. Stay tuned!
Read more at Renjin's blog or subscribe to the blog's RSS feed.
